as porcentagens no começo de cada exercício são uma maneira de indicar o seu grau de dificuldade. Mas não se apegue muito a esses valores: talvez você ache fáceis alguns que eu julgo como difíceis — e vice versa!
pode-se usar recursos do módulo scipy.optimize à vontade.
para fazer gráficos rápidos e ajudar a encontrar graficamente raízes, use recursos online como os do www.desmos.com.

Exercício 1: Iteração nos métodos da bissecçao e de Newton

dificuldade: 30%

Para resolver a equação $x=\cos(x)$ com uma precisão de 8 algarismos significativos, quantas iterações serão necessárias no método da bissecção se começarmos delimitando a raiz no intervalo $\left[0.5,\ 1.0\right]$? E no método de Newton-Raphson, começando com o chute inicial $x_0=1$?

Exercício 2: Método das Secantes

dificuldade: 40%

Implemente o método das secantes em python e use-o para achar todas as raízes da função

\[f(x) = x^2 - 4 x + \cos x\]

Exercício 3: Catenária

dificuldade: 25%

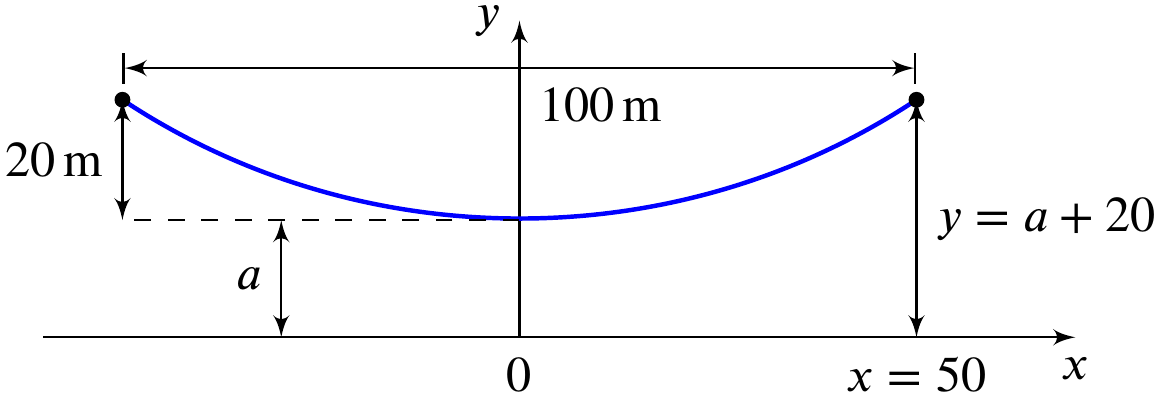
Cabos usados em pontes e linhas de transmissão suportam o próprio peso uniformemente distribuído e assumem um formato conhecido por catenária, expresso por

\[y(x) = a \cosh\left(\frac{x}{a}\right)\]

sendo $a$ um comprimento definido na figura e

\[\cosh \theta = \frac{e^\theta+e^{-\theta}}{2}\]

a função cosseno hiperbólico.

Considere que o cabo está suspenso entre dois pontos distantes 100m um do outro, com uma máxima deflexão de 20m. Além disso, o cabo tem um peso específico de $w=50\,$N/m.

Determine as tensões mínima e máxima suportadas pelo cabo, que acontecem, respectivamente, no meio ($x=0$) e nas extremidades ($x = \pm 50\,$m) e são dadas por $ T_\mathrm{min}= w a $ e $ T_\mathrm{max}= w (a+20)$.

Exercício 4: A equação de Kepler

dificuldade: 25%

Muitos métodos numéricos, incluindo o de Newton-Raphson, foram criados explicitamente para resolver a equação de Kepler:

\[E = M + e \sin E\]

onde $M$ é a anomalia média, $e$ é a excentricidade e $E$ é a anomalia excêntrica de um corpo em órbita elíptica segundo as leis da gravitação ($M$ e $E$ são ângulos usualmente dados em graus). Resolva a equação para $E$ no caso em que $M=5$° e $e=0.100$, com uma precisão de $10^{-6}$ graus. Não esqueça de converter $M$ para radianos antes de começar!

Exercício 5: Calha semicilíndrica

dificuldade: 25%

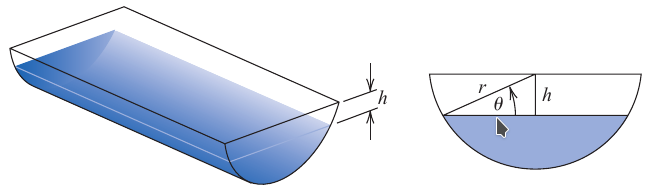
Uma calha de comprimento $L=10$m tem uma seção transversal constante na forma de um semicírculo de raio $r=1$m, como na figura abaixo:

Quando a calha está cheia com $V=12.4\,$m$^3$ de água, encontre $h$, a altura até a borda, usando a expressão

\[V = L \left[ \frac{1}{2} \pi r^2 -r^2 \arcsin\left(\frac{h}{r}\right) - h \sqrt{r^2-h^2}\right]\]

Exercício 6: Aplicação financeira

dificuldade: 25%

Numa certa aplicação financeira de capitalização, o usuário deposita mensalmente uma certa quantia fixa $P$ para receber uma taxa de juros $j$ ao mês de acordo com a fórmula

\[A = \frac{P}{j} \left[ (1+j)^{m}-1 \right]\]

em que $A$ é o montante acumulado ao final de $m$ meses. Um engenheiro gostaria de contar com 750000 reais ao final de 20 anos, mas só pode investir mensalmente 1500 reais. Qual é a menor taxa de juros para que isso seja possível?

Exercício 7: Queda com resistência do ar

dificuldade: 25%

Um objeto de massa $m = 0.25$kg, inicialmente em repouso, é solto de uma altura $h_0 = 300$m. Devido à resistência do ar e à gravidade, a altura do objeto no instante t é

\[h(t) = h_0 - \frac{m g}{k} t + \frac{m^2 g}{k^2} \left( 1 - e^{-k t/m} \right)\]

onde $g = 9.80665$m/s² é a aceleração da gravidade e $k = 0.1$kg/s é o coeficiente de resistência do ar. Encontre, com uma tolerância de 0.01s, o tempo que o objeto leva para atingir o solo.

Exercício 8: Arco e flecha

dificuldade: 40%

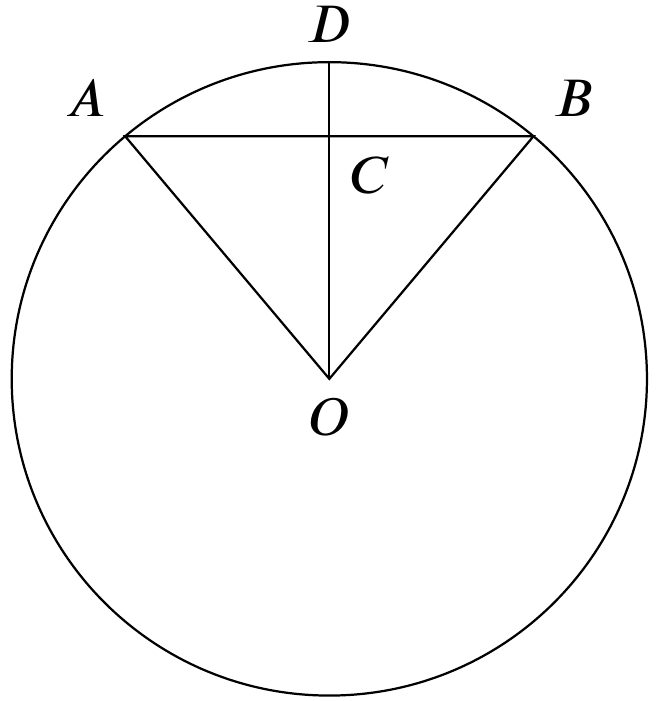
A figura representa um círculo de centro em $O$ em que a corda $AB$ mede 10cm e o arco $ADB$ (ao longo da circunferência) mede 12cm. Determine o comprimento da flecha $CD$, sendo $C$ o ponto médio de $AB$. Dica: tente descobrir primeiro o ângulo $A\hat{O}C$ e o raio do círculo.

Exercício 9: Escadas

dificuldade: 50%

Duas escadas, de comprimento $L_1$ e $L_2$, estão apoiadas às paredes de um beco de largura $W$, como na figura.

As escadas se interceptam a uma altura $H$ do chão. Determine $W$ se $L_1=15\,$m, $L_2=10\,$m e $H=4\,$m.

Página atualizada em 12-11-2020 13:18