Primeira Lista

• dificuldade: 10%
• utiliza:  

A maioria dos anos tem 365 dias. No entanto, o tempo necessário para a Terra orbitar o Sol é na verdade um pouco maior que isso. Para corrigir essa diferença, um dia extra, 29 de fevereiro, está incluído em alguns anos, ditos bissextos. As regras para determinar se um ano é ou não um ano bissexto são as seguintes:

Escreva um programa que leia um ano do usuário e exiba uma mensagem dizendo se ele é ou não um ano bissexto. Você consegue pensar num algoritmo mais eficiente, que faça em média menos testes?

Dicas para responder à pergunta final:

• Veja que o algoritmo proposto no enunciado testa inicialmente se um número é múltiplo de 400. Apenas um em 400 números é múltiplo de 400. Portanto, 399 de 400 (99.75%) não passam no primeiro teste e vão para o segundo.
• Similarmente, um a cada 100 números é múltiplo de 100, então 99 de 100 (99%) não passam pelo segundo teste e vão para o terceiro.
• Assim, em média, o algoritmo proposto faz muito mais comparações do que o necessário. Repensando os testes a serem feitos, é possível reduzi-los em número. Por exemplo, se você começar com o teste ano % 4 != 0, 3 de 4 casos resultam em True, ou seja, esse é o único teste que você precisaria fazer em 75% dos casos.

# Entrada de dados

ano = input('Digite o ano: ')

# Código - algoritmos

ano = int(ano) # convertendo ano de string para int

if ano % 400 == 0:  # é múltiplo de 400
    resultado = True
elif ano % 100 == 0:  # é múltiplo de 100
    resultado = False
elif ano % 4 == 0:  # é múltiplo de 4
    resultado = True
else:  # não é múltiplo de 4
    resultado = False

# Saída de dados

if resultado == True:
    res = 'é'
else:
    res = 'não é'

s = f'{ano} {res} bissexto' # mensagem formatada
print(s)

if ano % 4 != 0:  # não é múltiplo de 4
    resultado = False
elif ano % 100 != 0:  # é multiplo de 4 mas não de 100
    resultado = True
elif ano % 400 != 0:  # é múltiplo de 100 mas não de 400
    resultado = False
else:  # é múltiplo de 400
    resultado = True

resultado = (ano % 4 == 0 and ano % 100 != 0) or ano % 400 == 0

resultado = bool((not ano % 4 and ano % 100) or not ano % 400)

• dificuldade: 20%
• utiliza:

Escreva um programa que, dada uma duração de tempo em segundos, calcule o número equivalente de dias, horas, minutos e segundos.

Por exemplo, 123554 segundos equivalem a 1 dia, 10 horas, 19 minutos e 14 segundos.

Dicas:

Nesse exercício, use os operadores // (divisão inteira) e % (resto de divisão). Alguns exemplos:

x = 18
y = x // 3 # retorna o int 6
y = x % 3 # retorna o int 0
y = x // 4 # retorna o int 4
y = x % 4 # retorna o int 2

t = 1423554  # tempo em segundos

s = t % 60  # segundos: 60 s = 1 min
t //= 60  # tempo restante em minutos
m = t % 60  # minutos: 60 min = 1 h
t //= 60  # tempo restante em horas
h = t % 24  # horas: 24 h = 1 dia
d = t // 24  # tempo restante em dias

print(f'{d}d {h}h {m}m {s}s')

# Teste da solução:
t = 60 * ( 60 * (d * 24 + h) + m) + s
print(f'{t}s')

• dificuldade: 20%
• utiliza:  

Se você tem 3 varetas, possivelmente de diferentes comprimentos, pode ou não ser possível ajeitá-las para que elas formem um triângulo. Por exemplo, se todos as varetas tiverem um comprimento de 6cm, pode-se facilmente construir um triângulo equilátero. No entanto, se uma vareta tem 6cm e as outras duas têm apenas 2cm, não dá pra criar um triângulo. Em geral, se qualquer uma das varetas é maior ou igual à soma das outras duas, elas não podem ser usadas para formar um triângulo. Caso contrário, o triângulo existe. Escreva um programa que determine se três comprimentos podem ou não formar um triângulo. O programa recebe 3 parâmetros e retorna um resultado booleano (True ou False).

arestas = input('a b c = ').split()
a, b, c = map(int, arestas)  # o comando map(f, L) aplica a função f à lista L

if a >= b + c or b >= a + c or c >= a + b:
  triangulo = False
else:
  triangulo = True

if triangulo:
  print(f'Triângulo {a, b, c} existe')
else:
  print(f'Triângulo {a, b, c} não existe')

• dificuldade: 10%
• utiliza:   

Monte um código que imprima os números de 1 a 100 mas, para múltiplos de 3, imprime trei ao invés do número; se é múltiplo de 5, imprime cinci; mas, se é múltiplo de 3 e 5 ao mesmo tempo, imprime cincisprezece (3, 5 e 15 em romeno).

N = 100
d1, d2 = 3, 5
f1, f2, f3 = 'trei', 'cinci', 'cincisprezece'

for n in range(1, N+1):
  if n % d1 == 0:
    if n % d2 == 0:
      print(f3)
    else:
      print(f1)
  elif n % d2 == 0:
    print(f2)
  else:
    print(n)

• dificuldade: 15%
• utiliza:   

Crie um programa que peça ao usuário um número e imprima todos os seus divisores. Se você não lembra o que é um divisor, é um número que divide outro sem deixar resto. Por exemplo, 13 é um divisor de 26 porque 26/13 não tem nenhum resto.

n = int(input('Digite um número:'))

print(f'Divisores de {n}:')
for d in range(1, n):
    if n % d == 0:
        print(d)

• dificuldade: 10%
• utiliza:   

O máximo divisor comum (MDC) de dois inteiros positivos, $n$ e $m$, é o maior número, $d$, capaz de dividir $n$ e $m$ sem deixar resto. Existem vários algoritmos para determinar $d$, incluindo o seguinte:

Ao final do algoritmo, $d$ sera o MDC de $n$ e $m$. Escreva um programa que leia dois inteiros positivos do usuário e use esse algoritmo para determinar e relatar seu máximo divisor comum.

# Entrada
m = int(input('m = '))
n = int(input('n = '))

# Algoritmo

# encontrando o menor valor
if m < n:
  d = m
else:
  d = n

# encontrando o MDC(m, n)
while m % d or n % d :
  d -= 1

'''
comentário:
veja que
while m % d or n % d:
é o mesmo que
while m % d != 0 or n % d != 0:
pois qualquer valor positivo significa True,
e qualquer valor zero ou negativo resulta em False
'''

# Saída

print(f'MDC({m}, {n}) = {d}')

• dificuldade: 10%
• utiliza:    

(MIT) Escreva um programa que conte o número de vogais numa string s composta unicamente de letras minúsculas. Por exemplo, se s = 'azcbobobegghakl', seu programa deve imprimir Número de vogais: 5.

• dificuldade: 30%
• utiliza:    

(MIT) Escreva um código para contar o número de vezes que a sequência 'bob' aparece numa string s composta unicamente de letras minúsculas. Por exemplo, se s = 'azcbobobegghakl', seu programa deve imprimir Número de ocorrências de bob: 2.

• dificuldade: 60%
• utiliza:    

(MIT) Escreva um código para imprimir a maior sequência em ordem estritamente alfabética de uma string s composta unicamente de letras minúsculas. Por exemplo, se s = 'azcbobobegghakl', seu programa deve imprimir Maior sequência em ordem alfabética: beggh. Em caso de empate, imprima apenas a primeira subsequência. Por exemplo, se s = 'abcbcd', seu programa deve imprimir Maior sequência em ordem alfabética: abc.

• dificuldade: 50%
• utiliza:     

Implemente um algoritmo para converter números em algarismos arábicos (por exemplo, 4, 18, 29, 98, 1746) em algarismos romanos (IV, XVIII, XXIX, XCVIII, MDCCXLVI). Limite-se aos valores de 1 a 3999. Se estiver inspirado, implemente a conversão de algarismos romanos para arábicos.

# DICIONÁRIOS
rom2arab = {'I': 1, 'V': 5, 'X': 10, 'L': 50, 'C': 100, 'D': 500, 'M': 1000}
arab2rom = {val: key for key, val in rom2arab.items()}  # invertendo r2a usando list comprehension

def det_simb(digit, pos=1):
  '''
    função auxiliar para determinar o símbolo
    correspondente ao dígito (digit: int)
    do número arábico na pos
    pos = 1   -> unidade
        = 10  -> dezena
        = 100 -> centena
  '''
  
  if digit <= 3:  # I, II, III ou X, XX, XXX ou C, CC, CCC
    return arab2rom[pos] * digit
  elif digit == 4:  # IV ou XL ou CD
    return arab2rom[pos] + arab2rom[pos * 5]
  elif digit == 5:  # V ou L ou D
    return arab2rom[pos*5]
  elif 6 <= digit <= 8:  # VI, VII, VIII ou LX, LXX, LXXX ou DC, DCC, DCCC
    return arab2rom[pos*5] + arab2rom[pos] * (digit - 5)
  else:  # IX ou XC ou CM
    return arab2rom[pos] + arab2rom[pos * 10]

def a2r(num):
  '''
    Conversão de número arábico num (int) para romano 
    válido para 1 <= num <= 3999
  '''
  
  arab = f'{num:04d}'
  rom = ''
  # dígito do milhar:
  d = int(arab[0])
  rom = arab2rom[1000] * d
  # dígito da centena:
  d = int(arab[1])
  rom += det_simb(d, pos=100)
  # dígito da dezena:
  d = int(arab[2])
  rom += det_simb(d, pos=10)
  # dígito da unidade:
  d = int(arab[3])
  rom += det_simb(d, pos=1)
  
  return rom

def r2a(rom):
  '''
    conversão de número em algarismos romanos rom (str) para arábicos (int)
  '''
  
  cm = rom[-1]
  num = rom2arab[cm]

  for c in rom[-2::-1]:  # lendo um caractere por vez, de traz para frente, começando do penúltimo
    if rom2arab[c] >= rom2arab[cm]:
      num += rom2arab[c]
    else:
      num -= rom2arab[c]
    cm = c
    
  return num


# TESTE: todos os inteiros de 1 a 3999
for A in range(1, 4000):
    R = a2r(A)  # de arábico para romano
    print(r2a(R), R)  # de romano para arábico

• dificuldade: 10%
• utiliza:    

Digamos que eu lhe forneça uma lista de números: a = [1, 4, 9, 16, 25, 36, 49, 64, 81, 100]. Escreva uma única linha em Python que gere uma nova lista apenas com os elementos pares de a.

• dificuldade: 15%
• utiliza:   

Escreva um programa que converta um número binário (base 2) em decimal (base 10). Seu programa deve ler o número binário do usuário como uma sequência de zeros e uns e exibir o número decimal equivalente, processando cada dígito da representação binária. Por exemplo, 1010011 (base 2) $\equiv$ 83 (base 10), obtido a partir da definição:

# Input
binario = input('Digite um número em base 2: ')

# Algoritmo

soma = 0
p = 1  # = 2**expoente

for digito in binario[::-1]:  # slicing para inverter a string
    soma = soma + int(digito) * p
    p = 2 * p

# Output
print(f'{binario} (base 10) = {soma} (base 2)')

• dificuldade: 15%
• utiliza:  

Escreva um programa que converta um número decimal (base 10) em binário (base 2). Leia o número decimal do usuário e use o seguinte algoritmo de divisão, exemplificado para o número 83 (base 10):

	83/2 = 41 resto 1
	41/2 = 20 resto 1
	20/2 = 10 resto 0
	10/2 = 5 resto 0
	5/2 = 2 resto 1
	2/2 = 1 resto 0
	1/2 = 0 resto 1

Os restos das divisões (começando do último valor) contém a representação binária do número, nesse caso 1010011 (base 2).

# Entrada

decimal = int(input('N (base 10) = '))

# Algoritmo

# inicialização das variáveis
quociente = decimal
binario = ''

'''
comentários:
- quociente vair receber, a cada iteração, o resultado da divisão por 2
- binário é uma string inicialmente vazia, que receberá os restos das divisões por dois
- usamos o operador concatenação de strings (+) para construir a representação binária
'''

while quociente > 0:
    resto = quociente % 2
    quociente = quociente // 2
    binario = str(resto) + binario

# Saída
print(f'{decimal} (base 10) = {binario} (base 2)')

• dificuldade: 30%
• utiliza:    

Uma das maneiras de se referir a cores em websites e outras aplicações é a notação RGB (red-green-blue): três inteiros $0 \le R,\,G,\,B \le 255$ como identificadores das tonalidades de vermelho, verde e azul, respectivamente, que, quando mescladas, fornecem a cor desejada. Ao invés de fornecer os três inteiros em base 10, no entanto, é comum usar base 16. Essa maneira de identificar cores é conhecida como código hexadecimal. Em base 16, precisamos de 16 caracteres para representar os “dígitos” de um número (veja que em base 2 precisamos de dois, e em base 10, de dez). Usualmente são escolhidos os caracteres 0–9, com os valores usuais, e portanto precisamos de mais seis caracteres para representar os “dígitos” de de 10 a 15. Usualmente usa-se as letras A–F. Por exemplo,

Números que em base 16 são formados por apenas dois caracteres equivalem aos números de 0 a 255 ($= 16 ^ 2 -1$) em base 10. Além disso, no código hexadecimal as três tonalidades são indicadas por uma única string de seis caracteres. Por exemplo, o código hexadecimal CD1F41 corresponde aos tons $R=205$, $G=31$ e $B=65$, como você pode conferir aqui. Esse sistema (ou seja, seis caracteres escolhidos do conjunto 0–9+A–F) é capaz de descrever $256^3=16\,777\,216$ cores diferentes, de 000000 (preto) a FFFFFF (branco). Com base nos exercícios anteriores sobre números binários, monte um algoritmo para converter uma string válida de seis caracteres representando uma cor em código hexadecimal para a notação RGB, ou seja, os três inteiros $0 \le R,\,G,\,B \le 255$ com as tonalidades de vermelho, verde e azul. Implemente também a conversão no sentido contrário, ou seja, dados três inteiros $R,\,G,\,B \in [0,\,255]$, determine o código hexadecimal da cor em questão.

• dificuldade: 30%
• utiliza:   

Calcule uma aproximação para $\cos x$ através da série

até que o módulo do último termo seja menor que $10^{-6}$. O usuário deve fornecer o valor de $x$. Não use a função fatorial, pois isso é desperdício de tempo de processamento, já que boa parte das operações para o cálculo de um termo da série já foi feita para o termo anterior!

import numpy as np


def cos_serie(x, tol=1.e-6, unid='rad'):

  '''
    cos_serie calcula cos(x) por série de Taylor com uma tolerância no número de termos

    entrada:
      - x (obrigatório): float de que se deseja calcular o cosseno
      - tol (opcional): módulo do útimo termo é menor do que isso
      - unid (opcional): unidade de x.
          Opções:
            - 'rad' (padrão): x em radianos
            - 'graus': x em graus
  '''

  x0 = x * np.pi / 180 if unid == 'graus' else x

  termo, soma = 1., 1.
  a, b = 2, 1
  while abs(termo) > tol:
    termo *= -x0*x0 / a / b
    soma += termo
    a, b = a+2, b+2

  return soma


# usando a função
x = float(input('x='))
print(f'cos({x}) = {cos_serie(x)}')

• dificuldade: 20%
• utiliza:  

Calcule as quinze primeiras aproximações para $\pi$ de acordo com a série

Novamente, não use uma função fatorial, é uma perda de tempo e de recursos computacionais!

'''
Solução usando for, e eliminando fatores de 4 da fórmula do enunciado:
(pi-3)/4 = 1/(2*3*4) - 1/(4*5*6) + 1/(6*7*8) - ...
é simplificada para
pi-3 = 1/(1*3*2) - 1/(2*5*3) + 1/(3*7*4) - ...
'''

soma = 3 # variável que vai receber as aproximações de pi
sinal = 1 # variável com o sinal dos termos da soma
for n in range(1, 16): # sequencia de 15 valores de 1 a 15
    soma += sinal / (n * (2 * n + 1) * (n + 1))
    print(n, soma)
    sinal = -sinal # alternando o sinal do termo

• dificuldade: 20%
• utiliza:   

Implemente o seguinte joguinho de computador: o usuário deve adivinhar um número de 1 a 100 “pensado” pelo computador (use a função randint() do módulo numpy.random). A cada palpite do usuário, o programa vai “cercando” o número, informando o intervalo $[a,\,b]$ em que ele se encontra. Acompanhe o seguinte exemplo, em que o número secreto é 42:

Adivinhe o número:
Está entre 0 e 100: 25
Está entre 25 e 100: 60
Está entre 25 e 60: 40
Está entre 40 e 60:

E assim por diante, até o usuário acertar. Não precisa de interface gráfica! Use a função input() para pedir ao usuário seu palpite (ou seja, crie uma TUI — text-based user interface). Qual é a melhor estratégia para ganhar o jogo no menor número de tentativas?

• dificuldade: 35%
• utiliza:    

Escreva um programa que leia uma data do usuário e calcule o dia seguinte. Por exemplo, se o usuário inserir valores que representem 18/11/2013, o programa deve exibir 19/11/2013. A data deve ser inserida em formato numérico com três declarações de entrada separadas, uma para o ano, uma para o mês e uma para o dia. Certifique-se de que o seu programa funcione corretamente para anos bissextos.

def fevereiro(ano):
    # retorna o no. de dias em fevereiro do ano
    return 29 if (not ano % 4 and ano % 100) or not ano % 400 else 28

# entrada de dados
d = int(input('Dia: '))
m = int(input('Mês: '))
a = int(input('Ano: '))
print(f'dia atual: {d:02d}/{m:02d}/{a}')

# durações de todos os meses
duracoes = {1: 31, 2: fevereiro(a), 3: 31, 4: 30, 5: 31, 6: 30,
            7: 31, 8: 31, 9: 30, 10: 31, 11: 30, 12: 31}

if d < duracoes[m]:  # não é o último dia do mês
    d += 1  # apenas incrementa o dia
elif m == 12:  # último dia do mês 12
    d = 1  # incrementa o ano
    m = 1
    a += 1
else:  # último dia dos meses 1-11
    d = 1  # incrementa o mês
    m += 1

# imprimindo o resultado
print(f'dia seguinte: {d:02d}/{m:02d}/{a}')

• dificuldade: 40%
• utiliza:     

Um dos primeiros exemplos conhecidos de criptografia foi usado por Júlio César, que precisava fornecer instruções escritas para seus generais, mas não queria que seus inimigos descobrissem seus planos se a mensagem caísse em mãos erradas. Como resultado, ele desenvolveu o que mais tarde ficou conhecido como Código de César. A ideia é simples mas, em consequência, não fornece proteção contra técnicas modernas de quebra de código. Cada letra na mensagem original é deslocada de 3 lugares. Por exemplo, A torna-se D, B torna-se E, C torna-se F, D torna-se G, etc. As últimas três letras do alfabeto são enroladas de volta do início: X torna-se A, Y torna-se B e Z torna-se C. Caracteres não alfabéticos ficam inalterados. Escreva um programa que implemente o Código de César. Permita ao usuário fornecer a mensagem e o valor do deslocamento (não necessariamente 3) e, em seguida, exiba a mensagem codificada. Garanta que seu programa codifique letras maiúsculas e minúsculas de modo coerente. Faça com que seu programa suporte também valores de deslocamento negativos, para que possa ser usado tanto para codificar quanto para decodificar mensagens.

Dicas

1. Os caracteres da Tabela ASCII correspondentes às letras A-Z e a-z estão, respectivamente, nas posições 65-90 e 97-122. Os algarismos de 0 a 9 correspondem às posições de 48 a 57.
2. Os seguintes comandos são úteis para esse (e outros) exercícios:
   • ord(c): retorna um int com a posição do caractere c na Tabela ASCII. Por exemplo, ord('A') retorna 65.
   • chr(n): retorna o caractere correspondente ao inteiro n. Por exemplo, chr(122) retorna 'z'.

• dificuldade: 20%
• utiliza:   

Escreva um programa que implementa o método de Newton para extrair a raiz quadrada de um número digitado pelo usuário. O algoritmo é o seguinte:

Quando o algoritmo é concluído, raiz contém uma aproximação da raiz quadrada de x. A qualidade da aproximação depende de como você define “bom o suficiente,” então adote o seguinte critério de parada: o valor absoluto da diferença entre raiz * raiz e x deve ser menor que $10^{-12}$.

'''
cálculo da raiz quadrada aproximada
usando método de Newton
com uma precisão de 1e-12
'''

x = float(input('Digite um número: '))

# Algoritmo: método de Newton para raiz quadrada
raiz = x / 2 # inicializar o palpite para a a raiz em x / 2
tolerancia = 1.e-12 # notacão científica: 1e-12 é igual a 1 * 10**(-12)
while abs(raiz**2 - x) >= tolerancia: # a função abs() retorna o módulo (valor absoluto) do seu argumento
    raiz = (raiz + x / raiz) / 2 # atualiza o valor do palpite para a raiz

print(f'A raiz quadrada de {x} é {raiz}')

• dificuldade: 20%
• utiliza:    

Escreva um programa para gerar uma senha aleatória. A senha deve ter um comprimento aleatório entre 7 e 10 caracteres (use a função randint() do módulo numpy.random). Cada caractere deve ser aleatoriamente selecionado das posições 33 a 126 na tabela ASCII. Sua função deve retornar a senha gerada aleatoriamente como único resultado, sem necessidade de entrada do usuário. Dica: a função chr() é útil para resolver esse exercício.

• dificuldade: 25%
• utiliza:     

Adapte o exercício anterior para gerar uma senha forte, tendo pelo menos 8 caracteres, pelo menos uma letra maiúscula, pelo menos uma letra minúscula, e pelo menos um número. Conte e exiba o número de tentativas que foram necessárias antes que uma senha forte fosse gerada.

• dificuldade: 20%
• utiliza:    

Interprete a saída da seguinte função, que usa uma propriedade conhecida como recursão:

def fatorial_recursivo(n):
    if n < 2:
        return 1
    else:
        return n * fatorial_recursivo(n-1)

• dificuldade: 30%
• utiliza:    

Usando recursão, implemente uma função para calcular o $n$-ésimo termo da série de Fibonacci,

que começa com $a_0=0$, $a_1=1$ e em que cada termo $a_n$ ($n \ge 2$) é calculado usando a equação recursiva

• dificuldade: 25%
• utiliza:    

Uma linha de melhor ajuste é uma linha reta que melhor se aproxima de uma coleção de $n$ pontos de dados. Neste exercício, vamos supor que cada ponto na coleção tem uma coordenada $(x_i,\,y_i)$, com $1\le i \le n$. A linha de melhor ajuste é representada pela equação $y = m x + b$, onde $m$ e $b$ são calculados usando as seguintes fórmulas:

onde os símbolos $\overline{x}$ e $\overline{y}$ são os valores médios de $x$ e $y$, respectivamente. Escreva um programa para ler os pontos contidos num arquivo-texto fornecido pelo usuário (use a função genfromtxt() do módulo numpy). Então calcule e exiba a linha de melhor ajuste. Por exemplo, se o usuário fornece as coordenadas $(1,\,1)$, $(2,\,2.1)$ e $(3,\,2.9)$, o seu o programa deve exibir y = 0.95 x + 0.1. Faça também um gráfico com os pontos e a linha de melhor ajuste usando as funções scatter() e plot() do módulo matplotlib.pyplot.

Para testar seu código, use os dados deste arquivo: dados-linear.csv

Um arquivo csv é um arquivo-texto em que os dados de cada linha estão separados por vírgulas (csv: comma separated values). Qualquer editor de texto é capaz de abri-los, e também programas de planilhas eletrônicas, como o M$Excel

• dificuldade: 20%
• utiliza:     

Considere o problema de identificar o máximo valor de uma coleção de inteiros, todos selecionados aleatoriamente no intervalo $[1,\,100]$. A coleção pode conter valores duplicados, e alguns dos números entre 1 e 100 podem não estar presentes. Pare um pouco e pense em como você lidaria com esse problema no papel. A maioria checaria cada número em sequência e perguntaria se o valor da vez é maior que o máximo dentre os anteriores. Se for, eles esqueceriam o máximo anterior e lembrariam o número atual como o novo máximo. Essa é uma abordagem razoável e resultará na resposta correta quando o processo for executado com cuidado. Implemente o método em python. Quantas vezes você esperaria precisar atualizar o valor máximo e lembrar de um novo número?

• dificuldade: 25%
• utiliza:    

O código Morse é um esquema de codificação que usa traços e pontos para representar números e letras. Neste exercício, você vai escrever um programa que usa um dicionário para armazenar o mapeamento de letras e números para código Morse, mostrado na tabela a seguir:

Seu programa deve ler uma mensagem do usuário. Então deve traduzir cada letra e número na mensagem para o código Morse, deixando um espaço entre cada seqüência de traços e pontos. Seu programa deve ignorar quaisquer caracteres que não sejam letras ou números. O código Morse para Hello, World! é mostrado abaixo:

....  .  .-..  .-..  ---   .--  ---  .-.  .-..  -..

• dificuldade: 15%
• utiliza:   

A Páscoa cai no primeiro domingo do ano após a lua cheia (mas não a lua cheia real, e sim de acordo com um antigo cômputo (computus) eclesiástico que nada mais tem a ver com a lua que vemos no céu: é apenas um algoritmo…) que acontece no ou imediatamente após o equinócio de março (considera-se sempre 21 de março como a data do equinócio, o que nem sempre é verdade, pois pode ser um ou dois dias antes…). Na prática, é mais fácil calcular a data da Páscoa usando o algoritmo de Meeus–Jones–Butcher:

O domingo de Páscoa será então no dia $p+1$ do mês $n$ (3: março, 4: abril). O algoritmo é válido para qualquer ano no calendário gregoriano, ou seja, a partir de 1583. Implemente-o em python e verifique aqui. Dica: não use o operador /, e sim // (divisão inteira) para as divisões.

def pascoa(ano):
    a = ano % 19
    b, c = ano // 100, ano % 100
    d, e = b // 4, b % 4
    f = ( b + 8 ) // 25
    g = ( b - f + 1 ) // 3
    h = ( 19 * a + b - d - g + 15 ) % 30
    i, k = c // 4, c % 4
    l = ( 32 + 2 * e + 2 * i - h - k ) % 7
    m = ( a + 11 * h + 22 * l ) // 451
    o = h + l - 7 * m + 114
    n, p = o // 31, o % 31
    return p + 1, n

# dicionário para converter mes de int para string
mes = {3:'Março', 4:'Abril'}

x = int(input('Ano: '))
d, m = pascoa(x)

# o formato 02d imprime um inteiro com 2 algarismos, com zeros à esquerda se necessário
print( f'Data da Páscoa em {x}: {d:02d} de {mes[m]}' )

• dificuldade: 30%
• utiliza:    

O triângulo de Pascal é uma tabela de números construída assim: o elemento da linha $i$ e coluna $j$ (com $0 \le j \le i$ e começando de cima, onde $i=j=0$) é dado por

As primeiras oito linhas (ou seja, até $i=7$) são mostradas abaixo:

  1
  1  1
  1  2  1
  1  3  3  1
  1  4  6  4  1
  1  5  10 10 5  1
  1  6  15 20 15 6  1
  1  7  21 35 35 21 7  1

1. Implemente um algoritmo para calcular as primeiras $n$ linhas do triângulo de Pascal.
2. Modifique o código para substituir os números ímpares do triângulo por 1 e os pares por 0. Use um valor alto de $n$ (algo em torno de 500) e salve o resultado numa matriz. Por fim, use o comando imshow() do módulo matplotlib.pyplot para exibir graficamente o resultado, que é muito parecido com o fractal chamado de Triângulo de Sierpinski (clique aqui e veja na Wikipedia).

• dificuldade: 40%
• utiliza:    

Um quadrado mágico é uma tabela de números em que a soma nas linhas, colunas e diagonais dá sempre o mesmo valor. Por exemplo, na gravura Melencholia I de Albrecht Dürer (1471–1528),

a soma dos números é sempre igual a 34 (o quadrádo mágico de Dürer serviu de inspiração para o nome e o logotipo da Editora 34). Outro exemplo simples é o seguinte, em que estão presentes todos os inteiros de 1 a 9 num quadrado $3\times3$:

  |---|---|---|
  | 8 | 1 | 6 |
  |---|---|---|
  | 3 | 5 | 7 |
  |---|---|---|
  | 4 | 9 | 2 |
  |---|---|---|

e a soma é sempre igual a 15.

Existe um algoritmo para criar quadrados mágicos de ordem ímpar $n$ (a ordem é o número de linhas = número de colunas), preenchidos por todos os inteiros de 1 a $n^2$:

Algoritmo:

Para ilustrar o uso do algoritmo, vejamos sua aplicação para gerar um quadrado mágico de ordem $n=5$:

• Comece com o passo i, colocando o número 1 na célula central superior do quadrado:

|---|---|---|---|---|
|   |   | 1 |   |   |
|---|---|---|---|---|
|   |   |   |   |   |
|---|---|---|---|---|
|   |   |   |   |   |
|---|---|---|---|---|
|   |   |   |   |   |
|---|---|---|---|---|
|   |   |   |   |   |
|---|---|---|---|---|

• Ao tentar usar o passo ii para inserir o próximo número (2), não temos célula acima e à direita da célula anterior (1). Temos então que usar o passo iii:

  |---|---|---|---|---|
  |   |   | 1 |   |   |
  |---|---|---|---|---|
  |   |   |   |   |   |
  |---|---|---|---|---|
  |   |   |   |   |   |
  |---|---|---|---|---|
  |   |   |   |   |   |
  |---|---|---|---|---|
  |   |   |   | 2 |   |
  |---|---|---|---|---|

• Alguns passos depois, usando os passos ii e iii, o quadrado estará assim:

|---|---|---|---|---|
|   |   | 1 |   |   |
|---|---|---|---|---|
|   | 5 |   |   |   |
|---|---|---|---|---|
| 4 |   |   |   |   |
|---|---|---|---|---|
|   |   |   |   | 3 |
|---|---|---|---|---|
|   |   |   | 2 |   |
|---|---|---|---|---|

• Como a próxima célula (1) já está ocupada, usamos o passo v para o próximo valor (6):

|---|---|---|---|---|
|   |   | 1 |   |   |
|---|---|---|---|---|
|   | 5 |   |   |   |
|---|---|---|---|---|
| 4 | 6 |   |   |   |
|---|---|---|---|---|
|   |   |   |   | 3 |
|---|---|---|---|---|
|   |   |   | 2 |   |
|---|---|---|---|---|

• Continuando por mais alguns valores, usando os passos ii, iii e v:

|----|----|----|----|----|
|    |    | 1  | 8  | 15 |
|----|----|----|----|----|
|    | 5  | 7  | 14 |    |
|----|----|----|----|----|
| 4  | 6  | 13 |    |    |
|----|----|----|----|----|
| 10 | 12 |    |    | 3  |
|----|----|----|----|----|
| 11 |    |    | 2  | 9  |
|--- |----|----|----|----|

• Atingido o canto superior direito, o próximo valor (16) vai abaixo dele, de acordo com o passo iv:

|----|----|----|----|----|
|    |    | 1  | 8  | 15 |
|----|----|----|----|----|
|    | 5  | 7  | 14 | 16 |
|----|----|----|----|----|
| 4  | 6  | 13 |    |    |
|----|----|----|----|----|
| 10 | 12 |    |    | 3  |
|----|----|----|----|----|
| 11 |    |    | 2  | 9  |
|--- |----|----|----|----|

• E agora continue com os passos ii, iii e v até terminar de preencher o quadrado:

|----|----|----|----|----|
| 17 | 24 | 1  | 8  | 15 |
|----|----|----|----|----|
| 23 | 5  | 7  | 14 | 16 |
|----|----|----|----|----|
| 4  | 6  | 13 | 20 | 22 |
|----|----|----|----|----|
| 10 | 12 | 19 | 21 | 3  |
|----|----|----|----|----|
| 11 | 18 | 25 | 2  | 9  |
|--- |----|----|----|----|

Lembre que o algoritmo só vale para valores ímpares de $n$. Existem muitos outros quadrados mágicos de mesma ordem, o algoritmo só fornece uma possibilidade.

1. Qual é a soma em cada linha, coluna e nas duas diagonais, em função de $n$? Responda a essa pergunta usando a cabeça, não o computador!
2. Implemente o algoritmo em python para montar e exibir um quadrado mágico de ordem $n$ ($n$ ímpar) com os números inteiros de 1 a $n^2$. A ordem do quadrado ($n$) deve ser fornecida pelo usuário.

• dificuldade: 80%
• utiliza:       

Ajude um rato a encontrar um pedaço de queijo num labirinto como o do desenho abaixo:

Exemplo de um labirinto

×

OK

Um labirinto desses pode ser representado por uma matriz retangular $L$, cujo elemento $\ell_{ij}$ vale $0$ ou $-1$, conforme a casa correspondente do labirinto seja uma passagem livre ou uma parede, respectivamente.

Um método geral para resolver esse problema consiste em marcar com o número $k$ ($k = 1, 2,\ldots$) todas as casas livres que estejam exatamente a $k-1$ passos de distância do queijo, pelo caminho mais curto possível. Suponha que, a cada passo, o rato possa se deslocar de apenas uma casa na vertical ou na horizontal. Então, rotula-se inicialmente a posição do queijo com $1$ e para cada $k\ge2$ examinam-se todas as casas livre do labirinto, marcando-se com $k$ aquelas ainda não marcadas e que sejam adjacentes a alguma casa marcada com $k-1$.

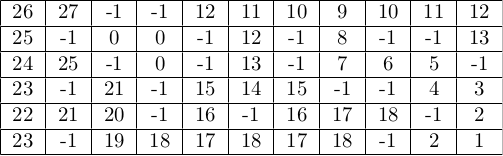
A marcação continua até ser atingido um valor $k$ (28 no exemplo abaixo) tal que nenhuma casa esteja em condições de ser marcada. Ao final da marcação teremos a seguinte matriz, supondo o queijo em (5,10), ou seja, no canto inferior direito:

Marcação do labirinto

×

OK

O caminho mais curto até o queijo pode então ser determinado, partindo-se da posição do rato e passando a cada etapa para uma casa adjacente cuja numeração seja menor do que a atual.

Por exemplo, partindo de (0, 0), i.e., o canto superior esquerdo, o rato precisará percorrer pelo menos 26 casas para chegar ao queijo: (0, 0), (1, 0), (2, 0), (3, 0), (4, 0), (4, 1), (4,2), …, (4, 10), (5, 10).

Dados o labirinto (matriz $L$) com elementos $0$ e $-1$ e as posições do rato e do queijo, determine o caminho mais curto que o rato deve percorrer até encontrar o queijo, se tal caminho existir.

Sugestão: escreva uma função que efetua a marcação (recebendo como argumentos a matriz $L$ e a posição do queijo) e uma outra que imprime o caminho (recebendo como argumentos a matriz $L$ já preenchida e a posição inicial do rato).

Com o código em mãos, teste a sua solução no seguinte labirinto:

Um labirinto mais complicado

×

OK

Baixe o arquivo com a matriz $L$ clicando no botão abaixo com o botão direito e escolhendo “Salvar link como…”

Baixe o arquivo labirinto-grande.txt

O arquivo labirinto-grande.txt é composto por 0’s e -1’s, formando um labirinto de 41 linhas e 101 colunas, com o rato inicialmente na posição (1,0) e o queijo em (39, 100).